Oefenvragen

De beste manier om je voor te bereiden is door de vragen van vorige jaren te bekijken:
Hieronder staan nog drie voorbeeldvragen: ze geven je een idee van de vragen die je tijdens de wedstrijd mag verwachten. De eerste twee zijn gelijkaardig en gemakkelijk, de laatste is eerder moeilijk (voor de categorie Masters).
(1) Teken de kerstboom (gemakkelijk)
Invoer:
1Uitvoer:
* *** ***** * *Invoer:
2Uitvoer:
* *** ***** ******* * *Invoer:
3Uitvoer:
*
***
*****
*******
*********
*
*
(2) Ascii-art (gemakkelijk)
Invoer:
1Uitvoer:
*** * * *** *** * * *** *** * * ***Invoer:
2Uitvoer:
***
* *
*** ***
* *
*** ***
* *
*** ***
* *
*** ***
* *
***
Invoer:
3Uitvoer:
***
* *
*** ***
* *
*** ***
* *
*** ***
* *
*** ***
* *
*** ***
* *
*** ***
* *
***
(3) Polyominos
Dominoblokjes hebben twee vierkantjes, en de blokjes uit tetris - genaamd tetrominos - hebben er vier: het zijn speciale gevallen van polyominos. In het algemeen is een polyomino een figuur die bestaat uit N vierkantjes die aan elkaar hangen doordat de vierkantjes een zijde gemeenschappelijk hebben.
Voor N = 2 bestaat er essentieel maar een
polyomino (een domino dus), namelijk

Je denkt misschien dat

een andere domino is, maar je krijgt die figuur door de vorige
te draaien over 90 graden, en dus is dat eigenlijk geen
nieuwe.
Voor N = 4 zijn er 7 verschillende tetrominos:
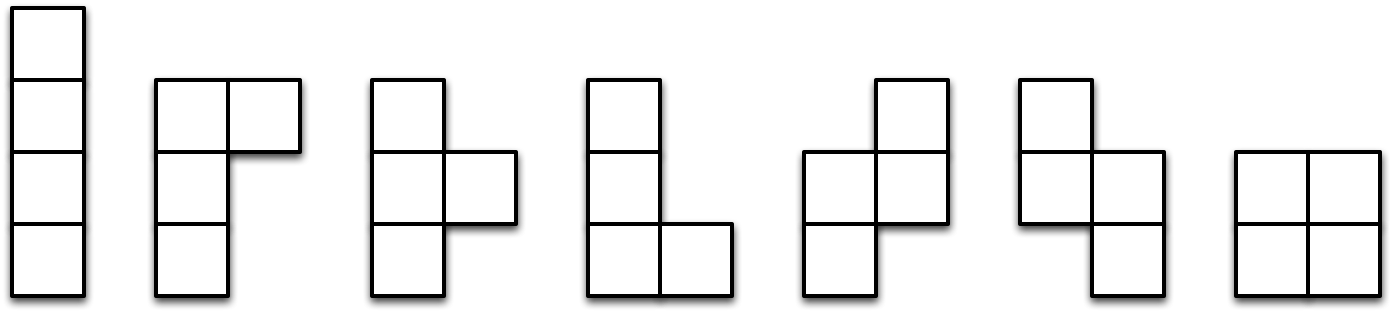
De opdracht: Schrijf een programma dat bepaalt hoeveel verschillende polyominos er zijn voor een gegeven N. Twee polyominos zijn verschillend indien ze niet door een draaiing van 90 of 180 graden in elkaar kunnen getransformeerd worden.
De invoer is een geheel getal N in [1,10], dus inclusief 1 en 10. De output is een geheel getal.
Invoer:
2Uitvoer:
1Invoer:
4Uitvoer:
7
Andere programmeerwedstrijden
Vragen van andere programmeerwedstrijden vind je op onderstaande websites: ze zijn meestal moeilijker dan wat wij voor je in petto hebben en kunnen dus dienen als oefenmateriaal.


